Pressure Drop effects on design of Plate Heat Exchangers

After calculating the exit temperatures in the rating calculation, or having determined the flow length in the sizing calculation, the pressure losses may be calculated. The pressure loss for each stream through the heat exchanger finned passages is calculated by

Δp=G2c2[(Kc+1−σ2)ρ1+2(1ρ2−1ρ1)+fρmAAc−(1−σ2−Ke)ρ2](1)$$\begin{array}{}\text{(1)}& \mathrm{\Delta }p=\frac{G_c^2}{2}\left[\frac{(K_c+1-{\sigma }^2)}{{\rho }_1}+2\left(\frac{1}{{\rho }_2}-\frac{1}{{\rho }_1}\right)+\frac{f}{{\rho }_m}\frac{A}{A_c}-\frac{(1-{\sigma }^2-K_e)}{{\rho }_2}\right]\end{array}$$

where subscripts 1 and 2 denote the entering and leaving fluid density.

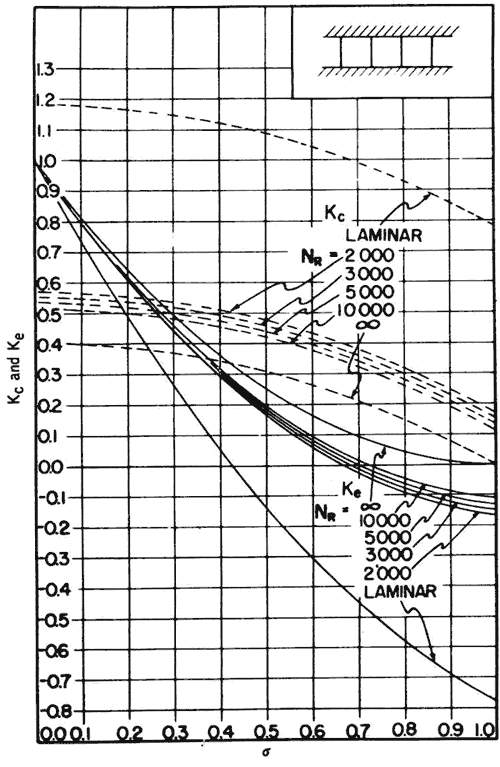
The terms of Equation 1 are entrance loss, flow acceleration loss, core friction, and exit loss, respectively. The K_c and K_e values depend on the cross-sectional flow geometry, σ and Re. Figure 1 gives K_c and K_e for a 1:1 ratio channel (Kays and London, 1984). Kays and London (1984) give similar curves for two other channel geometries (parallel-plate channel and triangular channel). The entrance and exit losses are normally < 10% of the total core loss, so the data of Figure 1 will cover most situations with adequate accuracy. The differences due to other channel configurations should cause only a second-order effect for most situations. Figure 1 is based on a uniform velocity entering the heat exchanger and fully developed flow in the core, and at the exit. This assumption is not valid for interrupted fin surfaces. In this case, Kays and London (1984) recommend the use of the Re = ∞ curves to evaluate K_c and K_e. In this case, all channel configurations have the same K_c and K_e values for Re = ∞. The calculation steps for the core pressure loss requires the information developed through step 6 of the rating calculation procedure. After calculation of the K_c and K_e values and the densities entering and leaving the core (ρ₁, ρ₂), the core Δp may be calculated using Equation 1.

Figure 1 Entrance and exit loss coefficients for multiple square channels with abrupt contraction entrance and abrupt expansion exit. Reynolds number is marked as N_R = Re, from Kays and London (1984)

The wavy and herringbone fin geometries are generically similar. Both have a “wavy” flow path, however, the herringbone wave form is that of a chevron and the wavy is in the form of a smooth wave. Dong et al. (2007) provide an empirical power law correlation for herringbone fins. Their correlation is based on data for 11 herringbone fin geometries. The j and f versus Re_Dh correlations are given by

j=0.0836Re−0.2309Dh(pfb)0.1284(pf2ew)−0.153(Lpw)−0.326(1)$$\begin{array}{}\text{(1)}& j=0.0836{\text{Re}}_{D_h}^{-0.2309}{\left(\frac{p_f}{b}\right)}^{0.1284}{\left(\frac{p_f}{2e_w}\right)}^{-0.153}{\left(\frac{L}{p_w}\right)}^{-0.326}\end{array}$$

Although the performance of the many different corrugation forms can vary considerably, the isothermal channel pressure loss in a plate heat exchanger can always be calculated from a friction factor type of equation:

Δp=2fLNpm˙2pde(1)$$\begin{array}{}\text{(1)}& \Delta p={\displaystyle \frac{2fL{N}_p{\dot{m}}^2}{p{d}_e}}\end{array}$$

Here L is the flow length given by the ratio of plate area and channel flow width.

A plate heat exchanger (PHE) comprises a pack of spaced corrugated plates arranged such that the two heat exchanging fluids flow through alternate spaces in the pack. The corrugations maintain the gap between adjacent plates which are sealed against each other. These are nowadays several different technologies to effect a seal between the plates and to maintain the pack in a compressed state.

Normally plates are pressed and expensive tools are required for their production. Unlike shell-and-tube units, plates are produced in a limited number of sizes and are never custom made to individual requirements. However, the flexibility of their arrangement enables a particular duty to be easily handled by the correct selection of standard components.

The big differences between the predicted and the measured pressure drops indicate that it is necessary to test all new patterns instead of relying on simulated predictions only

Pattern A plate is an asymmetric plate designed to have a low pressure drop. It is mainly used for liquid and steam processes.

The investigated angles of flow direction for pattern A. Normal flow direction being an angle of 0°

This pattern was tested for different directions of the flow since these can cause misdistribution of the medium throughout the channel. Due to lack of the sample plates only the steam side was tested. 

The two graphs (fig. 5 and 6) show that the predictions of the pressure drop made were too low and that the pressure drop increases with the angle of the direction of the flow

Figure 5: Fanning s friction factor for different inflow angles of water on the steam side of a pattern A channel 

                                                   Pattern A, Steam side: 0 degrees 

  Figure 6: A comparison of the predicted and measured values for the direction of the current flow

The pattern B plates can be arranged to make three different channels: narrow (NH), wide (SH) and medium (SS). The pressure drops in these were compared to the predicted ones. The results include the comparison for the heat transfer areas as well as for the whole channels

                  Figure 7: The predicted and the measured values for the pattern B SH channel

                 Figure 8: The predicted and the measured values for the pattern B NH channel

               Figure 9: The predicted and the measured values for the pattern B SS channel

The graphs show the same difference in tendencies for the heat transfer areas as for the whole channels. The second thing to be noted is that although they all come from the same plate the different channels show different pressure drop tendencies.

The pressure drop over several channels instead of just one should also be examined. The pressure drop for several channels is not necessary just a multiple of one channel.

Typical velocities in plate heat exchangers for waterlike fluids in turbulent flow are 0.3-0.9 m/s but true velocities in certain regions will be higher by a factor of up to 4 due to the effect of the geometry of the plate design. All heat transfer and pressure drop relationships are based on either a velocity calculated from the average plate gap or on the flow rate per passage.

Figure 2 illustrates the effect of velocity on pressure drop and film coefficient. The film coefficients are very high and can be obtained for a moderate pressure drop.

One particularly important feature of the plate heat exchanger is that the turbulence induced by the troughs reduces the Reynolds number at which the flow becomes laminar. Typical values at which the flow becomes laminar varies from about 100 to 400, according to the type of plate. The friction factor is correlated with:

where y varies from 0.1 to 0.4 according to the plate and B is a constant for the plate.

One other field suitable for the plate heat exchanger is that of laminar flow heat transfer. It has been previously pointed out that the exchanger can save surface by handling fairly viscous fluids in turbulent flow because the critical Reynolds number is low. Once the viscosity exceeds 20-50 cP, however, most plate heat exchanger designs fall into the viscous flow range. Considering only Newtonian fluids since most chemical duties fall into this category, laminar flow can be said to be one of three types:

1. Fully developed velocity and temperature profiles (i.e., the limiting Nusselt case);
2. Fully developed velocity profile with developing temperature profile (i.e., the thermal entrance region); or
3. The simultaneous development of velocity and temperature profiles.

The first type is of interest only when considering fluids of low Prandtl number, and this does not usually exist with normal plate heat exchanger applications. The third is relevant only for fluids such as gases, which have a Prandtl number of about one.

For type 2 correlations for heat transfer and pressure drop in laminar flow are in the form

(2)

where

• Nu = Nusselt number (αd/λ.),
• Re = Reynolds number (Vdρ/η),
• Pr = Prandtl number (c_pη/λ) ,
• η/η_p = Sieder Tate correction factor

and

(3)

where f is the friction factor and a is a characteristic of the plate.

From this correlation it is possible to calculate the film heat transfer coefficient, for laminar flow. This coefficient, combined with that of the metal and the calculated coefficient for the service fluid together with the fouling resistance, are then used to produce the overall coefficient. As with turbulent flow, an allowance has to be made to the Log Mean Temperature Difference to allow for either end-effect correction for small plate packs and/or concurrency caused by having concurrent flow in some passes. This is particularly important for laminar flow since these exchangers usually have more than one pass. 

Owing to particular geometry of plate corrugation Reynolds value in a PHE from laminar to turbolent regime is 200, while in a Shell & Tube  typical value is 1,500.

Plate Heat Exchangers design software is evaluating heat transfer area for a required duty with relevant LMTD assuming a proper K value and later on is going to verify if calculated plates/channels are able to match max pressure dop. In negative case software is adding plates/channels to reach amount of channels able to get pressure drop design/calculated.

Estimation of pressure drop through simulation is not always accurate (especially in case of high viscosity fluids or non newtonian fluids) there as thumb rule is better to keep some margin when pumps should be selected in order to have enough prevalence of the pump in the circuit.